Modelling Fish Schools
We are interested in the stochastic-dynamics of finite-sized fish schools to understand the underlying interactions that result in the collective behaviour observed. This work was done in collaboration with Dr Vishwesha Guttal (CES, IISc) and his lab and Dr Richard Morris (EMBL Australia).
Individual fish behaviour is probabilistic in nature: it spontaneously changes direction while swimming, it aligns with randomly chosen neighbours, it moves towards a group of selected neighbours to stay cohesive while maintaining a certain comfortable inter-fish distance. When the size of the school is small enough (<100), the behaviour at the level of the school is not deterministic. In the experiments conducted in Vishu’s lab (with juvenile Etroplus suratenesis, in a circular tank of 180 cm diameter and 10 cm depth: quasi-2D for the swimming fish), we find that there are periods when the fish school stays polarized, periods when the school mills or shows disordered motion. Hence, from the recorded information of the motion of the fish, an order parameter characterizing the alignment of the school (vector average of the heading-directions) is computed as a function of time. The resultant is a noisy time series that has information on the probabilistic nature of the underlying interactions.
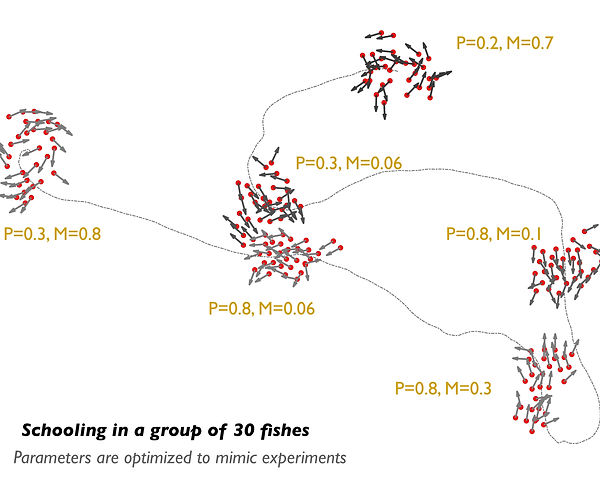
Simple agent-based models can be constructed to simulate the dynamics of fish schooling: spatial and non-spatial. A kinetic Monte Carlo approach can be employed to update the change in the directions of the heading of the fishes, based on the rates of the different reactions/interactions they exhibit. Agents will asynchronously change directions and time evolution of the positions. Rates at which the fish carry out their behavioural interactions are identified by posing the problem as an optimization problem where the objective is to reduce the Kullback–Leibler divergence between the probabilities of the magnitude of normalized group velocities in the model and data. We use a genetic algorithm (GA) to find a solution to the optimization problem and estimate the rates of interaction/reaction of the fish in the school. The agent-based models have large degrees of freedom: from swarming to highly polarized to disordered schools can be achieved based on the rates of interactions. In addition to the above-mentioned characteristics, spatial models show an additional degree of freedom where schools can be cohesive or non-cohesive. Hence, while implementing the GA, it is important to add a term to achieve cohesivity in the school.
Fishes orient, by changing direction based on the configuration of their neighbours. A canonical model for this interaction involves the fish choosing a direction that is the average of the directions of the neighbours. However, there is a reason to believe, from the study of the mesoscale statistics of the system, that the interaction would be a simple pairwise copying interaction where a fish chooses a random neighbour and copies its direction. One should note that a copying interaction requires only a small cognitive load unlike performing an average. The orientation interaction model is written down in a manner where depending on the parameter “k”; the interaction can be an averaging interaction when k=N-1, while k=1 corresponds to a pairwise interaction. GA identifies the best set of rates of the interaction and other parameters characterizing the interactions that give a good match between the data and simulation. We allow GA to find the ‘k’ for which the objective function is minimized. It is fascinating to note that GA always picks a pairwise copying interaction (k=1) over the canonical averaging interaction (Vicsek-like and its variants; k>1) which is the most commonly used interaction in the field of collective phenomena.